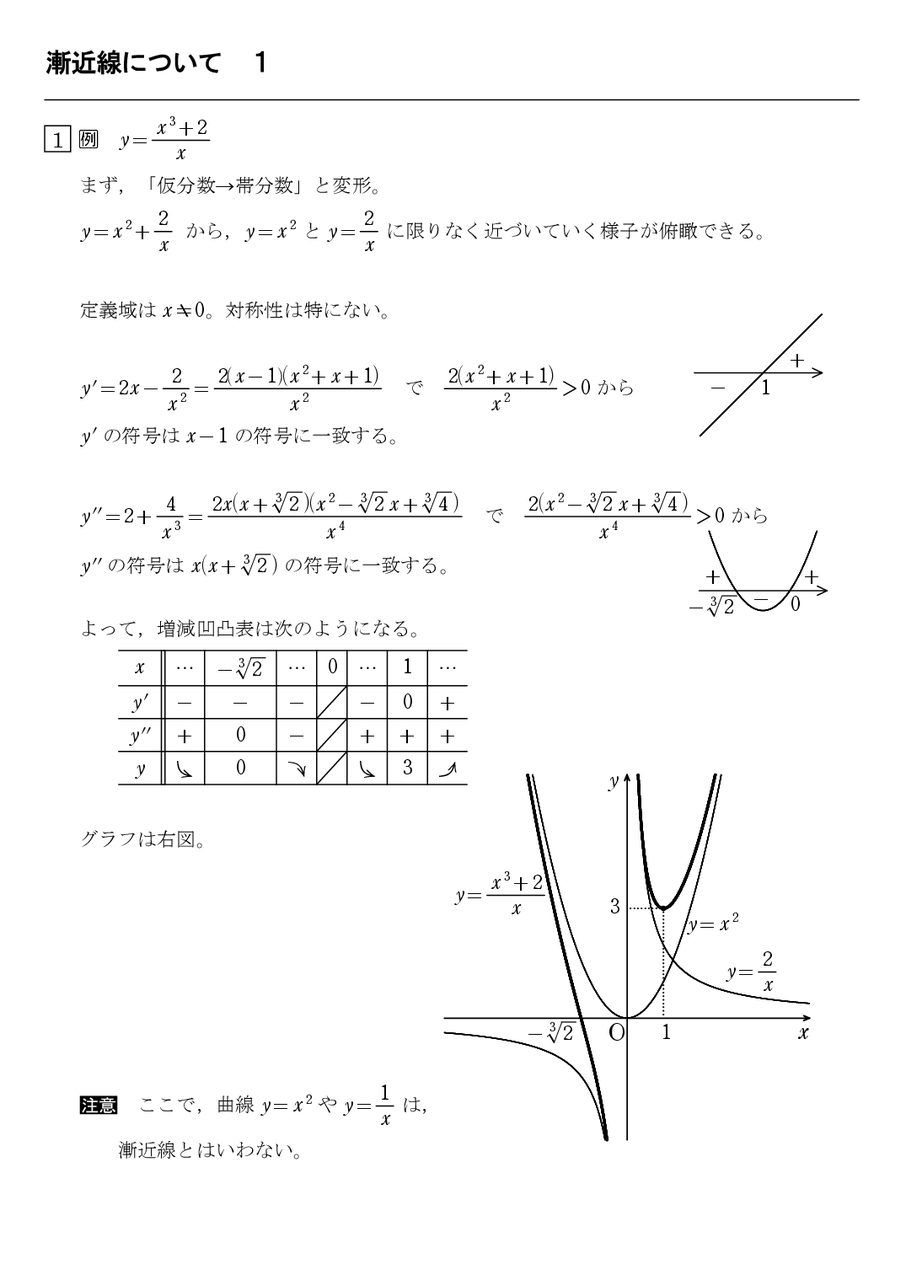
性質1 定義域(xのとりうる範囲)は実数全体,値域(yのとりうる範囲)は,正の実数全体。 性質2 1<a のとき,単調に増加する。つまり, 0<a のとき,単調に減少する。つまり, 性質3 指数関数 y=a x のグラフは,点(0,1)を通り,x 軸はその漸近線(その直線に限りなく近づいていくが,決して交わる (e^2x1) / (e^x2) の漸近線を求めよという問題があります。xはわかったのですが、 y軸と平行な漸近線の求め方がわかりません。答えは y= 1/2のようです。解き方を、教えてください。 xy平面上において、y軸と平行な漸近線を求め3 漸近線の求め方 31 軸に平行な漸近線の求め方 32 軸に平行でない漸近線の求め方2STEP 321 STEP1 の極限を調べる→傾きチェック 322 STEP2 代入する 4 漸近線の有無の判別方法 41 チェック① 軸に平行でない漸近線があるか 42 チェック② 不連続な点が
漸近線 Wikipedia
漸近線 求め方 log
漸近線 求め方 log- 2つ目は: (g⚪︎f) (x) "3つ"の関数の合成とその手順 (STEP1)まずf (x)とg (x)を合成し、 (STEP2)つぎにその合成関数とh (x)を合成する 逆関数とは 具体例とグラフ・性質 逆関数の求め方2ステップと注意点 step1 (x=)の形にし,xについて解く step2xとyを数学のコツ なものだが その log f (x) の項が発散する場合は y=ax+b タイプの漸近線はない <y=axbタイプの漸近線があるとき> y=f (x) の f (x) が1次式以下の場合 ただし必ずあるとは限らない <y=axbタイプの漸近線の求め方> ①傾きを求める



漸近線の方程式
こんにちは、 @kz_morita です。 今回は、アルゴリズムの評価軸である計算量、そしてよく使われるオーダー記法についてまとめていきます。 アルゴリズムとは? アルゴリズムというワードはよく聞くことが多いと思いますが、以下のように定義されていることが多いようです。逆三角関数の微分法 マクローリン展開 偏微分 == 漸近線の方程式 == ※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります関数が定義されず, x→1 のとき y→±∞ となります.このとき, x=1 が漸近線になります.(図1.ただし,図1にはもう一つ横向きの( x 軸に平行な)漸近線もありますが,これについては(2)で解説します.) 例12 y=tan x における x= , y=log x における x=0 のように
求めたいのは🔴の極限で log🔴が♾に行くことがわかりました。 なので🔴は0にいきます。 考え方の書き方としては log Xが♾に行く時、logの中身である真数Xは0に行くって考えてます。 これがいつもと逆から求めているっていうことの意味です制御系の特性を決めるのは一巡伝達関数 e K(s) P(s) y e からy までの周波数伝達関数 Y(s)=P(s)K(s)E(s) 実際の設計 P(s) に極・零点を追加,定数ゲインを変更 追加した極・零点や定数ゲインを集めてK(s) とする 浅井 徹 (名古屋大学) ボード線図のしくみ 分数関数とは? グラフや微分・積分、不等式の解き方 21年2月19日 この記事では、「分数関数」についてわかりやすく解説していきます。 グラフの書き方や不等式の解き方、微分・積分の計算なども説明しますので、この記事を通してぜひマスターして
4つ目の記事 数Ⅲlogを含む関数の漸近線 y=f(x)の漸近線の求め方を先に書いておこう。 ちなみにここで言う漸近線とは「直線」であり、 漸近線を求めることはその直線y=axbの 傾きaと切片bを求めることである。 ①傾きを求める漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。 単元 積分, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方,log,logarithm見て頂い 漸近線の求め方について x^22y^2=1 このときの漸近線の求め方を教えてください。 解答では x^22y^2=0 より y=±x/√2 になっているのですが なぜ x^22y^2=0 をしたことで漸近線が求められるのでしょうか?



2



対数 Wikipedia
(1) 次の関数のグラフの漸近線を求め,そのグラフをかけ。 ① = 3 −2 1 ② = 2 3 (2) 2つの関数 = 4 −1 , =3 −2について,次の問いに答えよ。 ① 2 つの関数のグラフの共有点の座標を求めよ。 ② グラフを利用して,不等式 4 −1漸近線の方程式 解説 高校の微分積分で漸近線の問題が登場するのは,微分法の応用として,「増減,極値,凹凸,変曲点,漸近線の方程式を求めてグラフの概形を書け」という場面です。 したがって,漸近線の方程式を単独で問うことはまれです。には流線と流跡線は一致します。流跡線は「流れの道筋」ともいわれます。第3話でお 話しするラグランジュの方法のところで再登場しますのでお楽しみに! t0 t1 t2 t3 流跡線 各時刻の流線 流跡線と流線 t0 t1 t2 t3 時刻t1 でこの位置に 来るとは限らない t = t1




対数関数の漸近線の求め方がわかりません Clearnote



対数関数
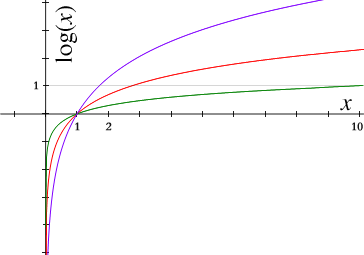
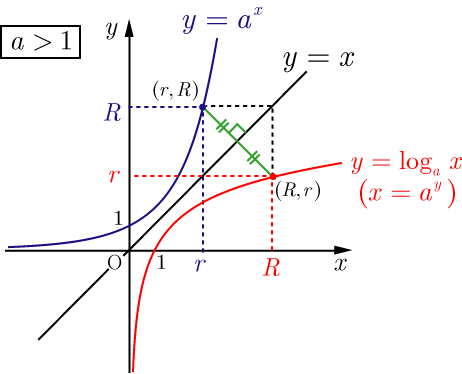
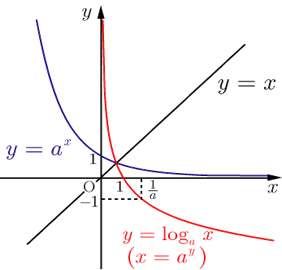
対数関数\(y=\log_a x\)は、 指数関数に直して考えるとわかりやすい。 底\(a\)が1以下の小数か、1以上か場合分けして考える。 底の値によらず、必ず点\((1,0)\)を通る。 \(y\)軸を漸近線にもつ。 指数関数とは、逆関数の関係にある。63 再帰方程式の解法 222–5 633 母関数と線形差分方程式 数列{an} の各項を係数とする級数 f(X)= ∞ i=0 aiX i をこの数列の ぼかんすう 母関数あるいは生成関数¶という.母関数を使って再帰方程式を解 くことができる.数列{ an} は,N からR への関数f:n → n に他ならな いことに注意する. ネイピア数 e e の定義に関するまとめ e e の意味は、「 x = 0 x = 0 の接線の傾きが 1 1 となるような指数関数 y = a x y = a x の底 a a 」 この定義から導ける式は、主に以下の 3 3 つであり、これらをすべて「 e e の定義式 」とする。 ① e = lim n → ∞ ( 1 1 n) n e
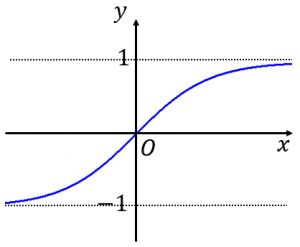



Tanhの意味 グラフ 微分 積分 具体例で学ぶ数学




数 微分法 漸近線 Y Ax B タイプ オンライン無料塾 ターンナップ Youtube
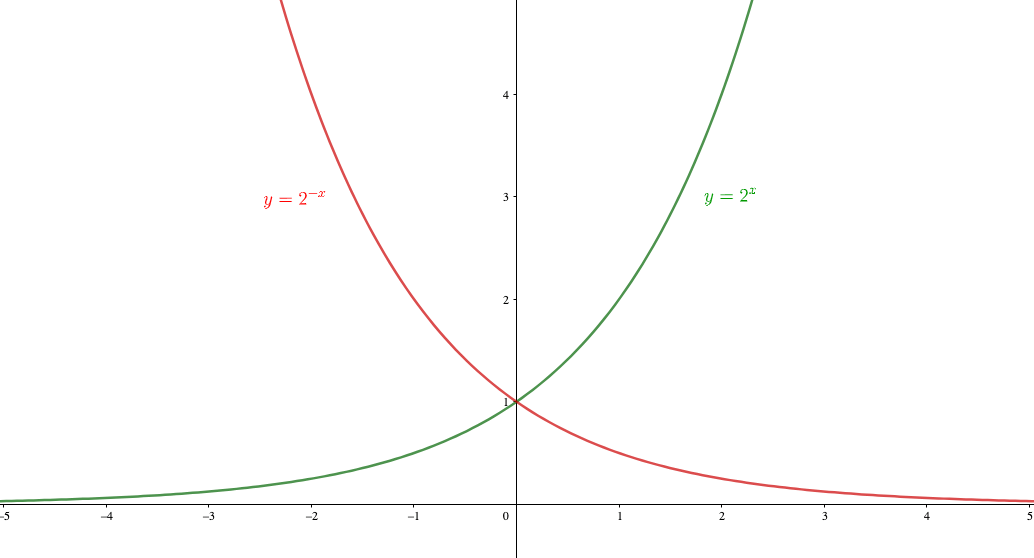
上図のように指数関数y=a x の漸近線はx軸です(y=a x はx軸に近づく)。指数、累乗の詳細は下記が参考になります。 指数とは?1分でわかる意味、読み方、指数法則、分数との関係 累乗とは?1分でわかる意味、読み方、計算、法則、マイナスとの関係 だから、y=logxの漸近線はy軸と同じになるのです。 では、y=log(x1)の場合はというと、(x1)=0が漸近線になります。 つまり、x=1が漸近線になるのです。 y=logxを、x方向に1だけずらしたグラフになります。 この時、x=1のところに、薄く漸近線と分かるように数学3の教科書に載っている公式の解説一覧 まとめ 更新日時 高校数学のラスボス,数3の教科書(新課程)に載っている公式(や定義など)を整理しました。 新課程になり数Cが消滅したせいで数3の分量が増えました。 目次 平面上の曲線 複素




対数関数とは何か 対数 と 関数 の基礎から応用までを工学博士が解説 Rikeinvest
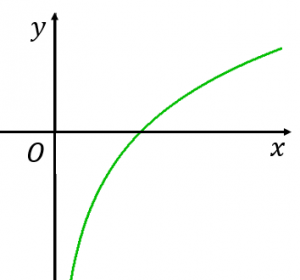



Y Logxのグラフの書き方 6つのポイント 具体例で学ぶ数学
目盛線があると両対数グラフであることが分かりやすくなります。 グラフスタイルで「スタイル4」を設定してみました。 両対数グラフらしくなりました。 上図は近似線を追加して、数式を表示していま指数関数・対数関数のグラフの確認 ★指数関数と対数関数のグラフの共通点や違いを確認しよう 1 a 1 y a a x 0 1 漸近11 関数のグラフ (ノート) このページにある内容は, こちらのスライド (会員向け)でわかり易く説明しています. 1. 微分係数と導関数 無料 ノート 2. 合成関数の導関数 無料 ノート 3. 逆関数の微分法 無料 ノート



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典
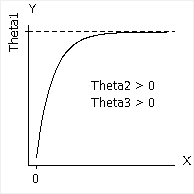



13 09 2 線形と非線形による曲線フィッティング 続 構造計画研究所 Minitabサポートセンター
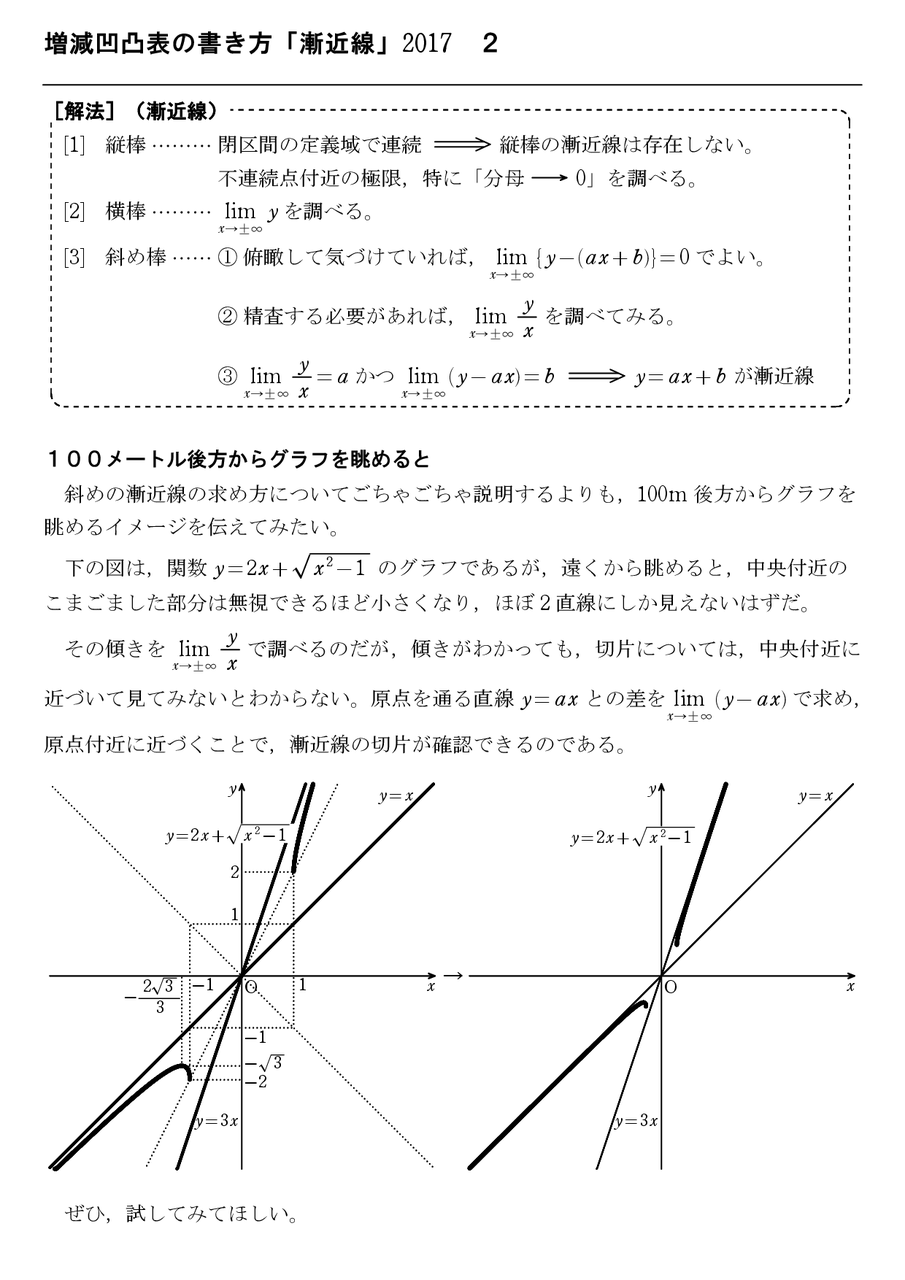
単元 積分, 「漸近線の描き方を一目にまとめました。 漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。」, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め漸近線の方程式 Geisya Internet ゲイシャインターネット;ダウンロード済み√ 漸近線 求め方 y 漸近線 求め方 y Inflec_pt = solve (f2, 'MaxDegree' ,3);これを利用して右側微分と左側微分を求め,その値が異なる点を漸近線として判定します。 const Range = 18;曲線に対する漸近線の求め方 f (x) = 3x2−5x x−2 f ( x) = 3 x 2




標準 微分と関数のグラフと漸近線 なかけんの数学ノート




対数関数のグラフと書き方 数学 理系ラボ
双曲線の漸近線の簡単な求め方と証明 楕円の接線を求める公式とその証明 放物線の準線・焦点と一般化 離心率の意味と関連する計算 楕円・双曲線の媒介変数表示の3通りの方法 NTT データ数理システムでリサーチャーをしている大槻 (通称、けんちょん) です。今回は計算量オーダーの求め方について書きます。 0 はじめに 世の中の様々なシステムやソフトウェアはアルゴリズムによって支えられています。Qi漸近展開に関するメモ Landau の記号と漸近展開 ver13 京都府立鳥羽高校定時制 稲葉芳成 はじめに この文章は, 大学初年度向けの微分積分のテキストである, 「三宅敏恒著『入門微分積分』培風館」を参考にして, 内容が平易でしかも有用である漸近展開に




漸近線の方程式




高校数学 双曲線のグラフ 1 映像授業のtry It トライイット
3334 (グラフの準備:漸近線の求め方 (指数対数関数)) 2 1,586 ビュー 見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください. ★の数は優先度です.★→★★→★★★ の順に取り組みましょう. 3241 3352 数学・算数 (e^2x1) / (e^x2) の漸近線を求めよという問題があります。 xはわかったのですが、 y軸と平行な漸近線の求め方がわかりません。 答えは y= 1/2のようです。




対数関数のグラフと書き方3ステップを解説




対数関数のグラフと書き方3ステップを解説




漸近線 の限界に漸近してみる Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー




分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す



1



Y Log X 1 3のグラフの書き方 漸近線の求め方 x軸と交わ Yahoo 知恵袋
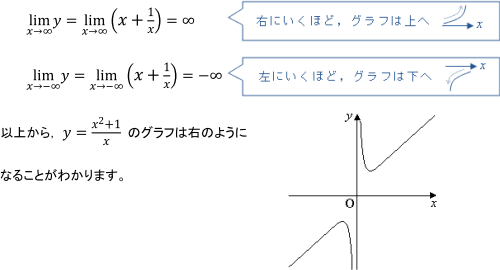



複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
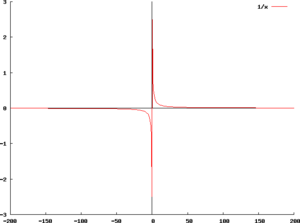



漸近線 Wikipedia
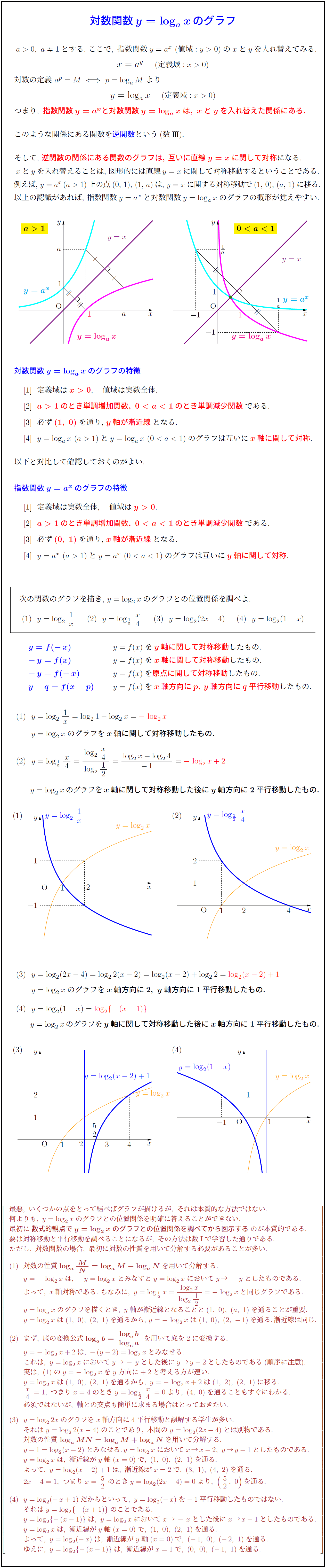



高校数学 対数関数y Log Axのグラフ 受験の月




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clearnote
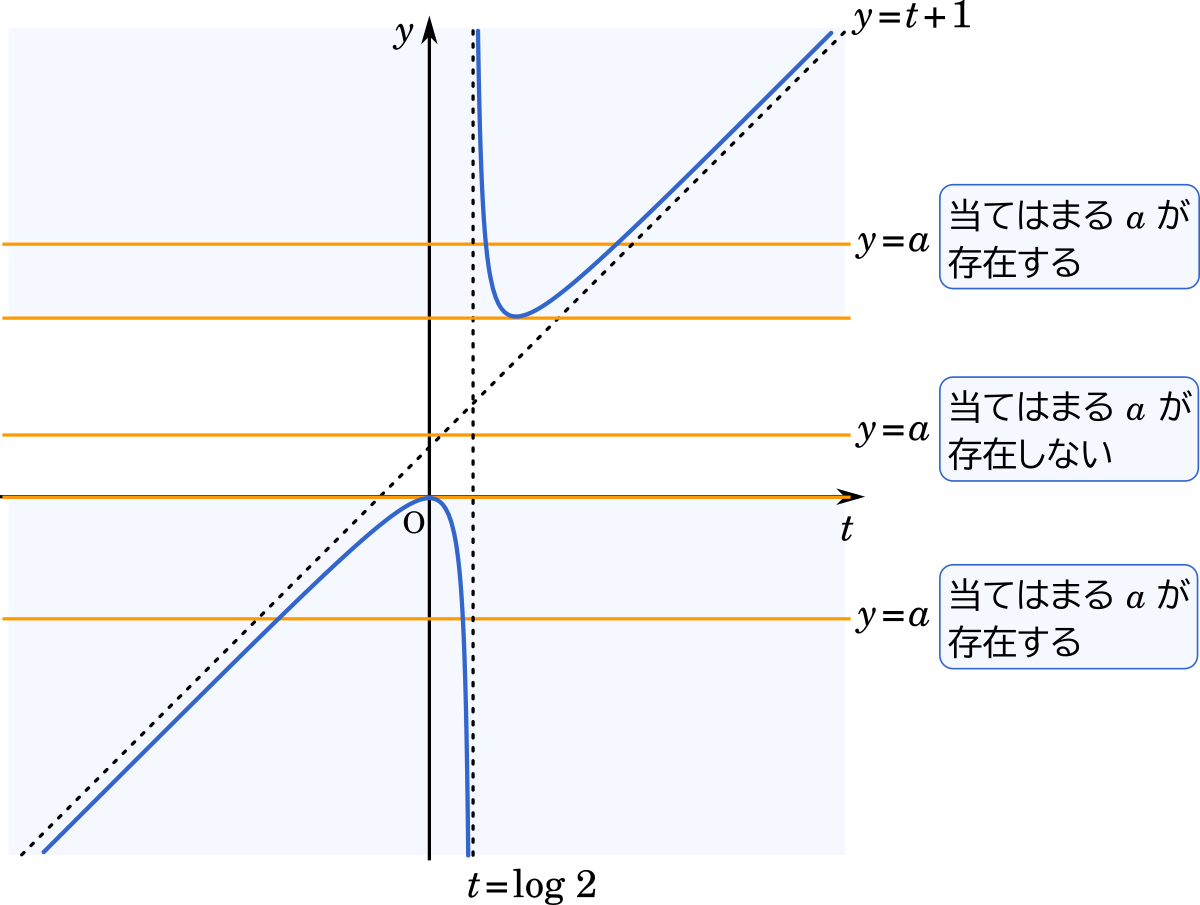



数iii微分 接線の座標の存在範囲 漸近線を求めてグラフの概形を描く 九州大 Mm参考書
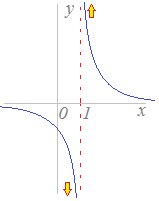



漸近線の方程式




授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット
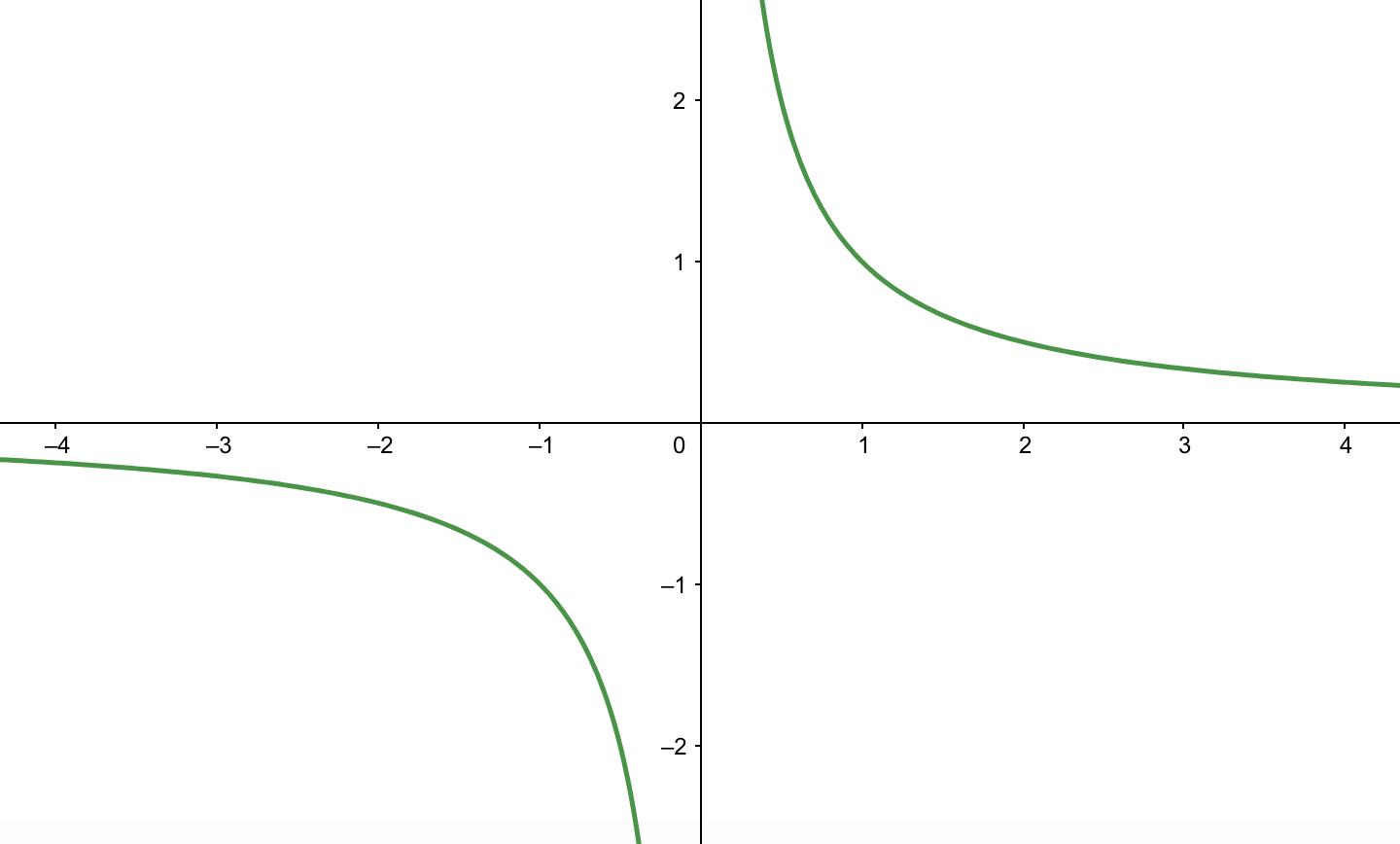



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




曲線 漸近線 求め方 2973 曲線 漸近線 求め方 Mbaheblogjpbmo0




漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clearnote



分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



Log2 Xー2 1のグラフの漸近線を教えてください Y Yahoo 知恵袋




漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



漸近線の求め方を教えてください Y Log E X E X Yahoo 知恵袋




1 の問題で なぜ対数関数のグラフは漸近線なのに最小値が存在するのでしょう Clearnote



漸近線 Wikipedia
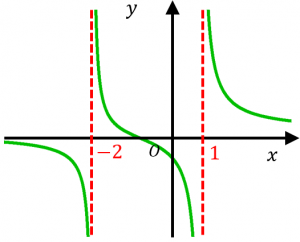



漸近線の求め方3パターン 具体例で学ぶ数学



2




分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法




指数 対数関数 グラフ編 ますますmathが好きになる 魔法の数学ノート




漸近線 身勝手な主張




数 微分法 漸近線 縦線タイプ オンライン無料塾 ターンナップ Youtube




対数関数の漸近線の求め方がわかりません Clearnote




対数関数のグラフと書き方3ステップを解説
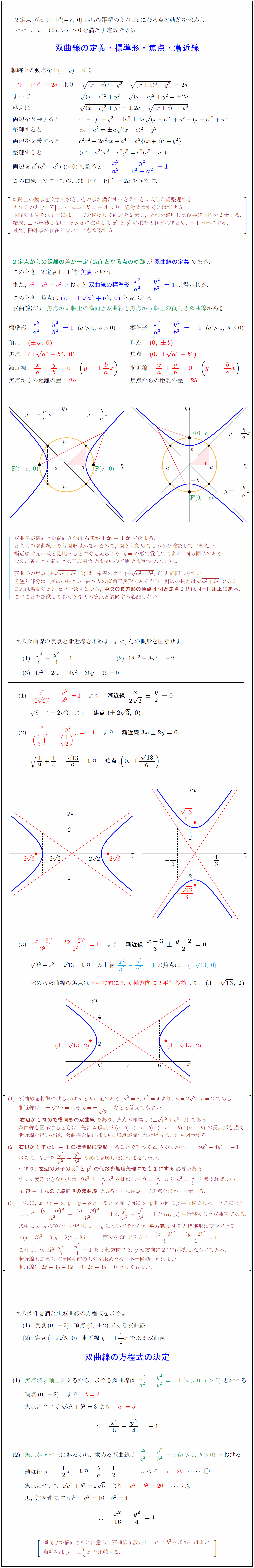



高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月



対数関数とは グラフや計算公式 微分積分や方程式 不等式 受験辞典




漸近線の求め方 高校数学 微分法の応用 14 Youtube



2




13 09 2 線形と非線形による曲線フィッティング 続 構造計画研究所 Minitabサポートセンター
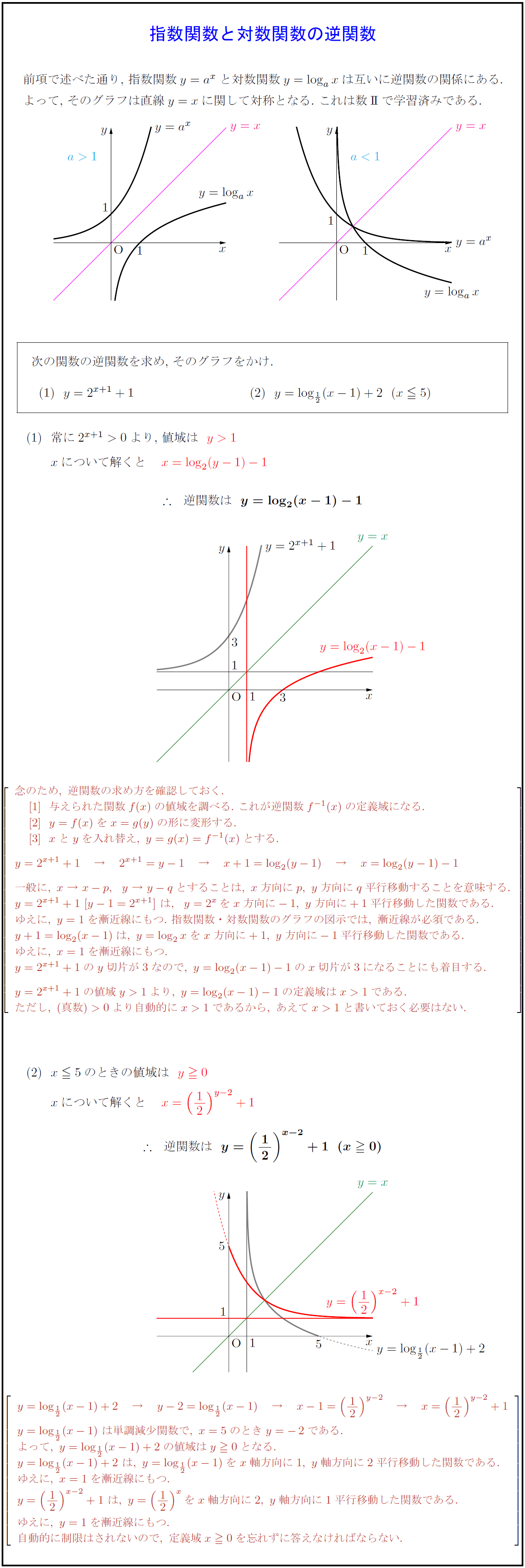



高校数学 指数関数と対数関数の逆関数 受験の月




Logのグラフ 書き方を解説 平行移動の場合には 数スタ




双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語




ねこ騙し数学
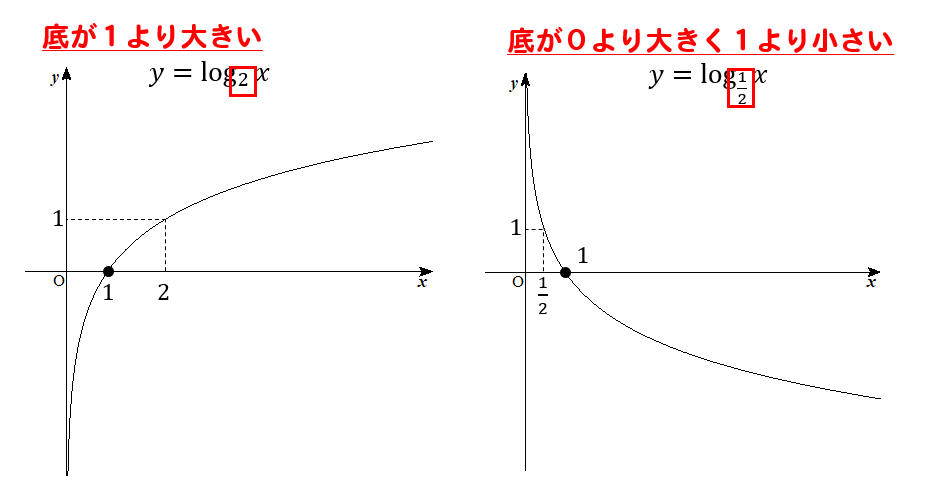



Logのグラフ 書き方を解説 平行移動の場合には 数スタ



増減凹凸表を書く手順 7 漸近線 1 怜悧玲瓏 高校数学を天空から俯瞰する



対数関数




対数関数のグラフと書き方 数学 理系ラボ




曲線 漸近線 求め方 2973 曲線 漸近線 求め方 Mbaheblogjpbmo0
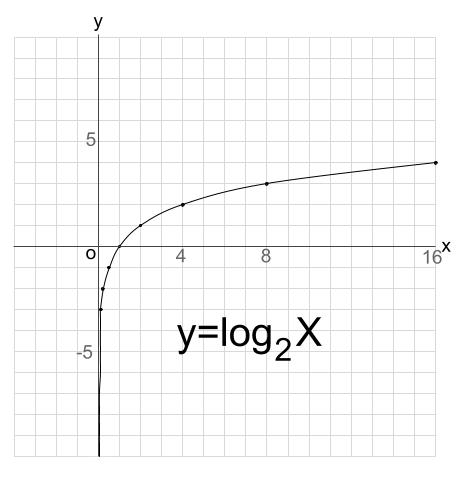



対数関数のグラフ 高校数学の無料オンライン学習サイトko Su




Y Log 2のx のグラフ Youtube




指数 対数関数 グラフ編 ますますmathが好きになる 魔法の数学ノート




一次分数関数のグラフと漸近線 高校数学の美しい物語




数3の グラフの凹凸と変曲点を求める問題での漸近線の求め方が あいうえおって Clearnote




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



Y Log X 1 X 2 2 Xの極値 変曲点 漸近線 Y切片の求め Yahoo 知恵袋



対数関数のグラフについて質問です Y 2log X 1 という問題で Yahoo 知恵袋




曲線 漸近線 求め方 2973 曲線 漸近線 求め方 Mbaheblogjpbmo0



増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する




対数関数のグラフと書き方 数学 理系ラボ




対数関数のグラフと書き方 数学 理系ラボ




漸近線 Wikiwand
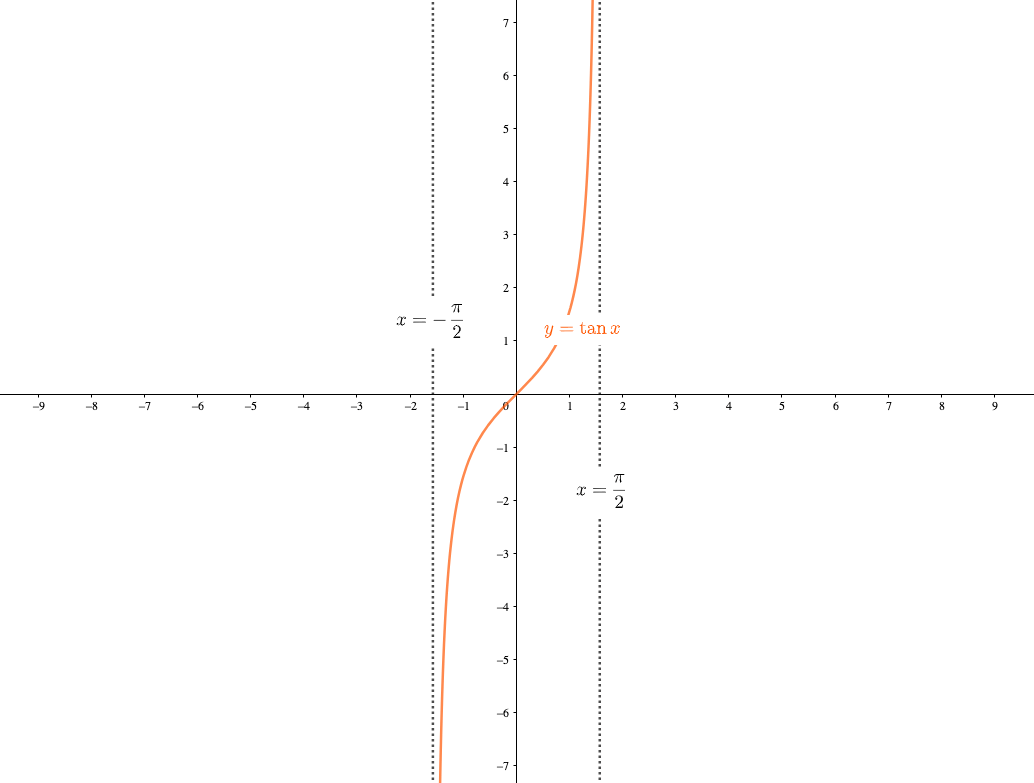



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




高校数学 分数関数のグラフ 2 映像授業のtry It トライイット



1



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書




対数関数のグラフ 大学受験の王道



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
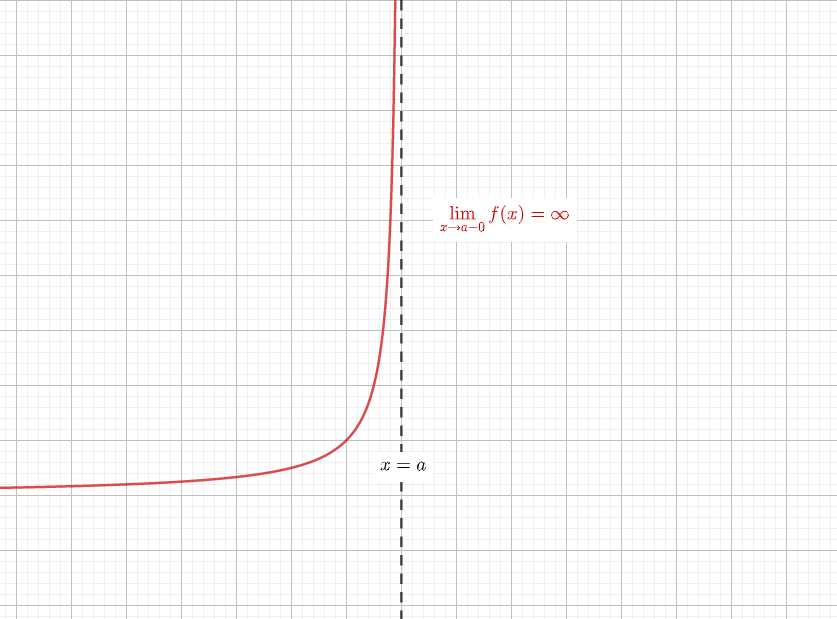



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




漸近線の方程式



Y Log X 1 3のグラフの書き方 漸近線の求め方 x軸と交わ Yahoo 知恵袋




対数関数とは何か 対数 と 関数 の基礎から応用までを工学博士が解説 Rikeinvest



2
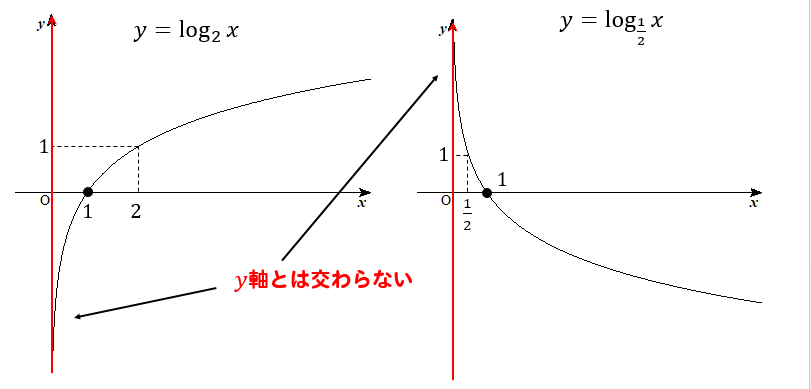



Logのグラフ 書き方を解説 平行移動の場合には 数スタ




自然対数 Wikipedia




漸近線 Wikiwand
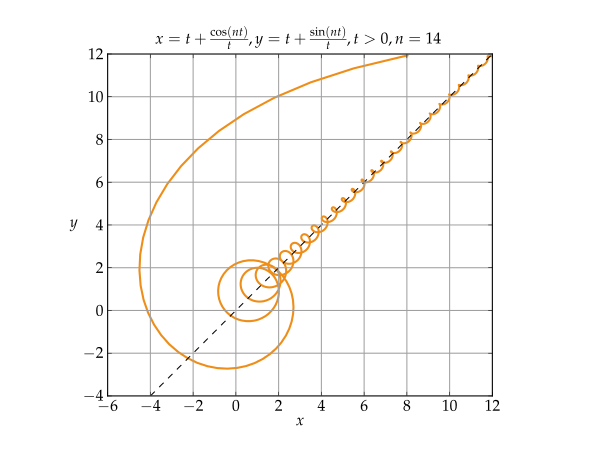



漸近線 Wikiwand




対数関数のグラフと書き方 数学 理系ラボ
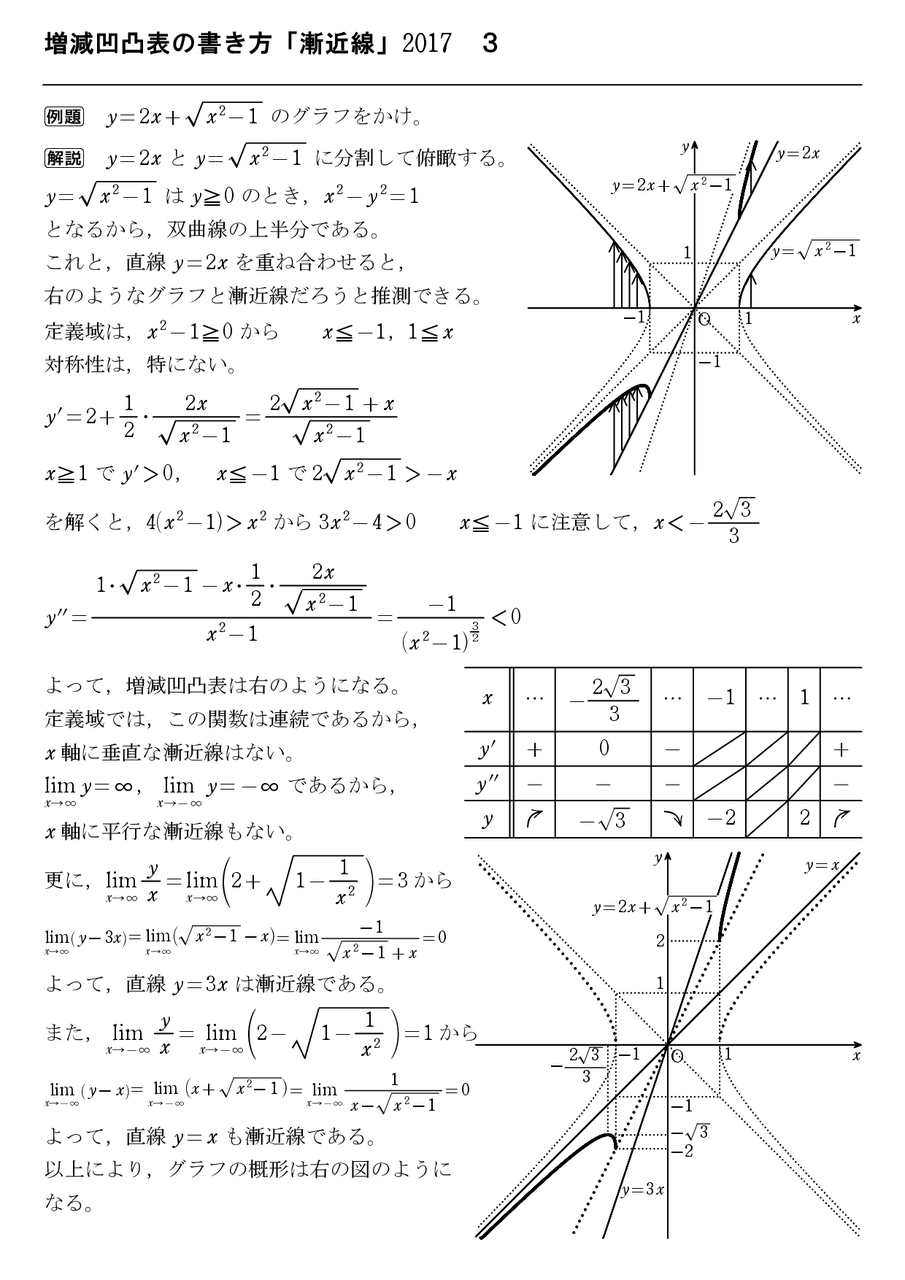



増減凹凸表の書き方 漸近線 17 3 怜悧玲瓏 高校数学を天空から俯瞰する



漸近線の方程式




曲線適合モデル




対数関数のグラフと書き方 数学 理系ラボ



曲線 漸近線 求め方 2973 曲線 漸近線 求め方 Mbaheblogjpbmo0



微分 グラフ 漸近 線 求め 方 21 U78l640 Iownyour Org




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
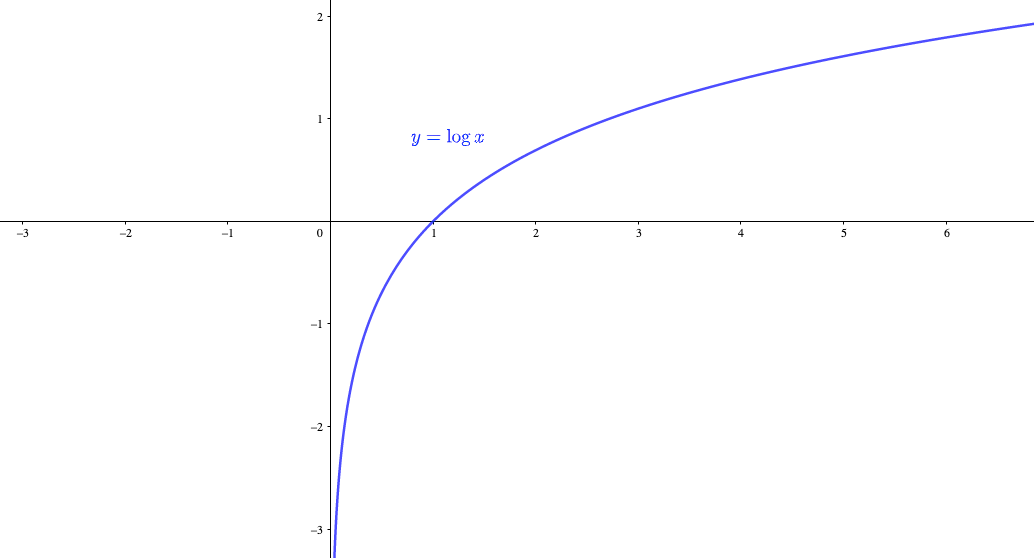



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




基本 双曲線と漸近線 なかけんの数学ノート




指数関数 対数関数のグラフ 数学の偏差値を上げて合格を目指す



3



1
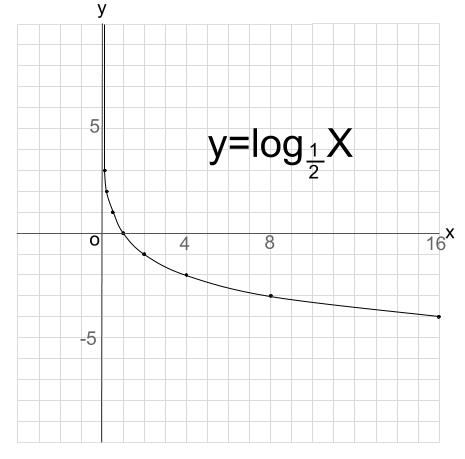



対数関数のグラフ 高校数学の無料オンライン学習サイトko Su



0 件のコメント:
コメントを投稿